[VIDÉO] Géométrie : L’œuf du pentagone

Published : 06/05/2021 21:49:37
Categories : Fabrication traditionnelle , Vidéos

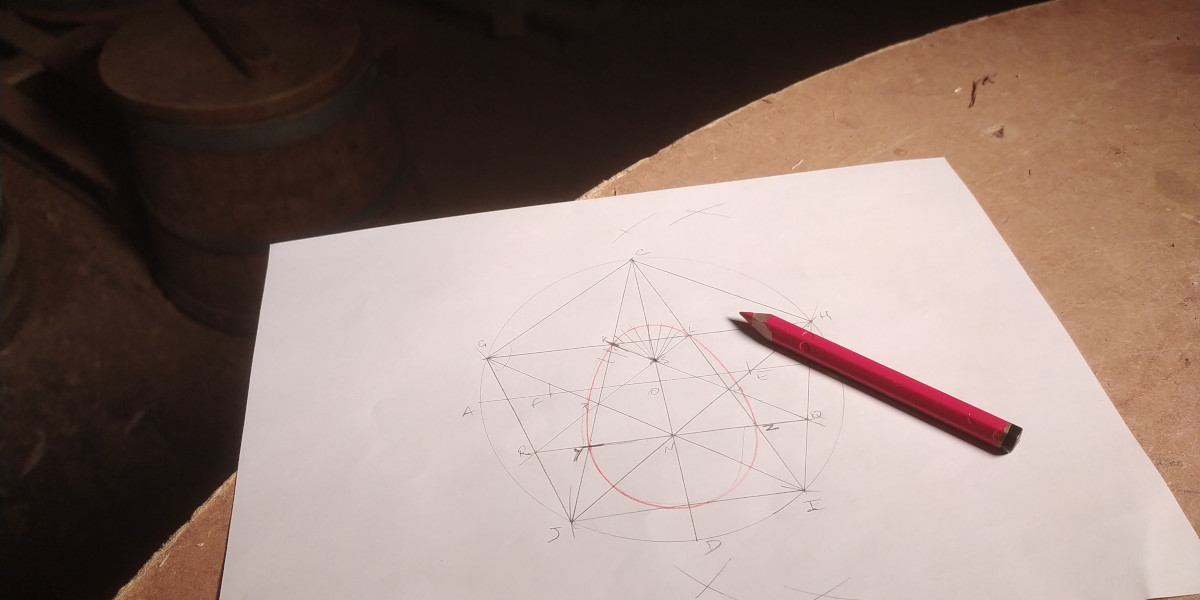
Nous avons vu récemment comment tracer une anse de panier à trois centres, tracé nous permettant de réaliser des fûts elliptiques avec une petite astuce géométrique fort utile. Voyons maintenant comment obtenir un ove, tracé qui comme son nom l'indique rappelle la forme d'un œuf, à l'aide d'une règle et d'un compas (et sans poule, c'est important). Ce tracé va nous permettre par exemple de fabriquer une baignoire ovoïde aux courbes très harmonieuses. Nous allons en fait voir deux tracés différents : l'œuf classique, simple mais efficace, et l'œuf du pentagone, qui sera un peu plus élancé que le premier et dont le trait aura pour base un pentagone régulier. Cette baignoire aura donc forcément quelques vertues magiques et quiconque s'y baignera obtiendra la vie éternelle... Peut-être...

L'œuf classique

Voyons tout d'abord ce tracé plutôt rapide et facile à réaliser. C'est l'œuf de base que vous avez probablement appris à tacer au collège. Mais si, souvenez-vous : on commence par tracer un cercle de centre O, on trace ensuite le diamètre [AB] de ce cercle, puis le diamètre [CD] perpendiculaire à [AB]. Reste maintenant à tracer les demi-droites [CB) et [DB) et nous y sommes. Voilà la base, le support qui va nous permettre de tracer l'œuf composé de trois arcs de cercles.

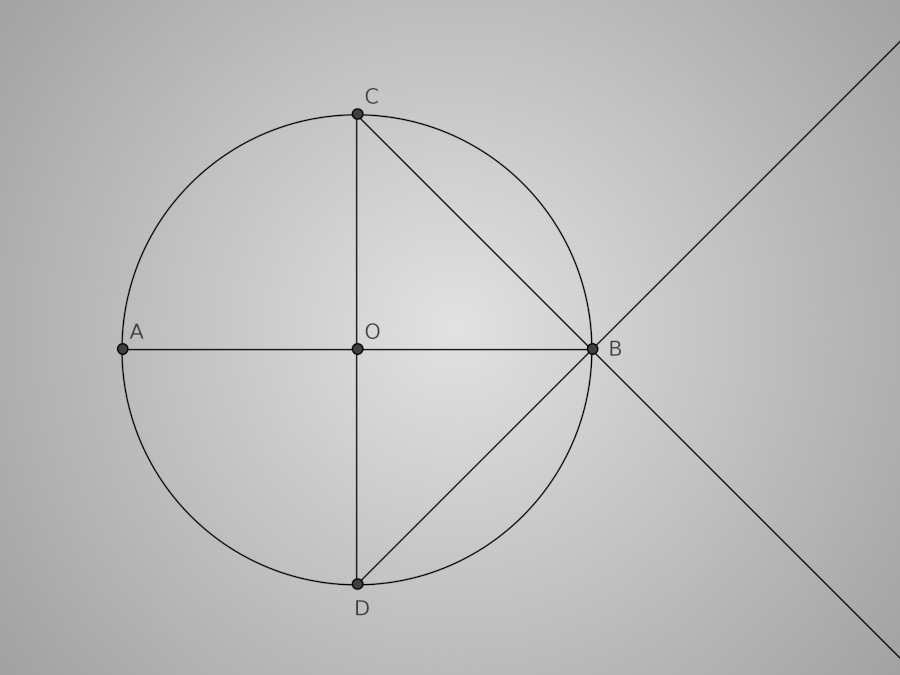
La base du tracé

Le premier est l'arc DC de centre O. Il a donc le même rayon que le premier cercle de la construction. Le diamètre de ce cercle nous donnera d'ailleurs la partie la plus large de la baignoire.

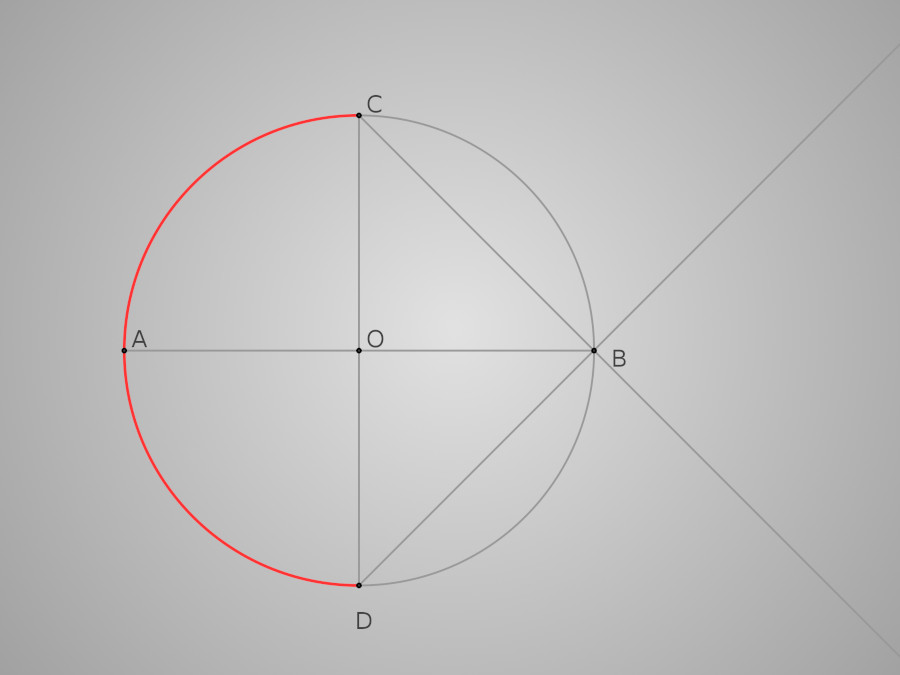
Premier arc

Les deux arcs suivants sont symétriques par rapport à (AB) et leur rayon est égal au diamètre du premier cercle : l'arc CE de centre D et de rayon [DC], E étant l'intersection de cet arc avec la demi-droite [DB). Puis l'arc DF de centre C et de rayon [CD], F étant l'inersection de cet arc avec la demi-droite [CB).

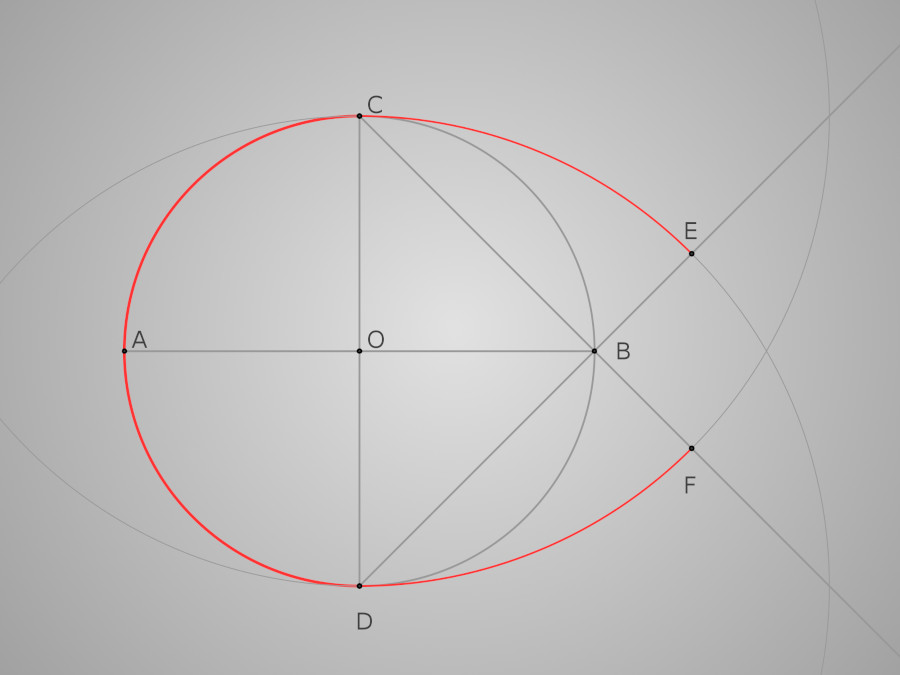
Deuxième et troisième arcs

Il ne nous reste plus qu'à compléter cet œuf avec l'arc EF de centre B et de rayon [BE]

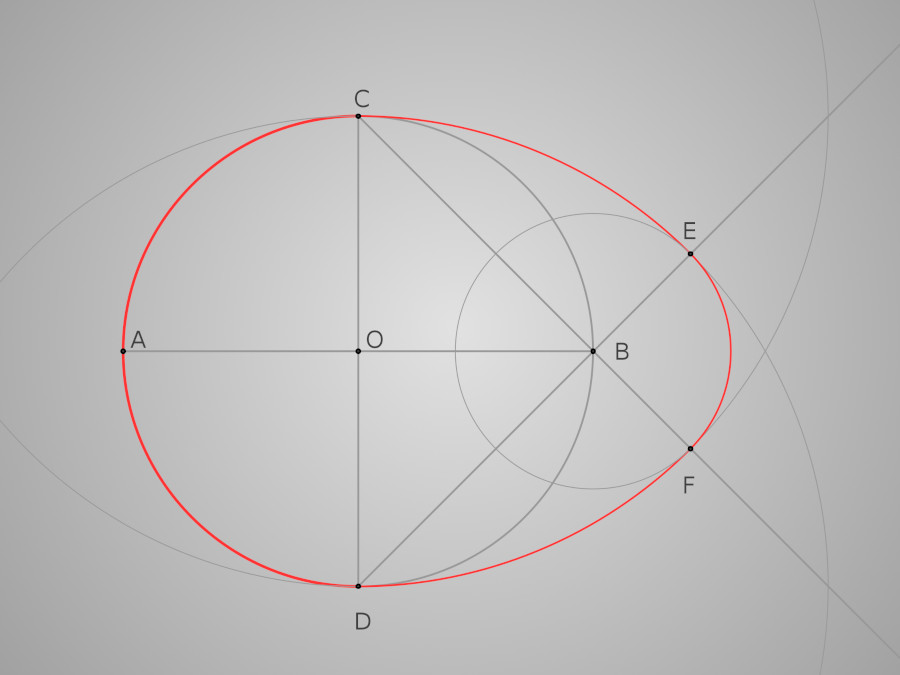
L'œuf complet

Le résultat final

Replaçons à présent quelques points et lignes de construction sur cette figure afin de déterminer par le calcul la longueur de l'œuf en fonction du rayon du premier cercle. Ça sera utile pour connaître les proportions de la baignoire avant de se lancer dans le tracé.

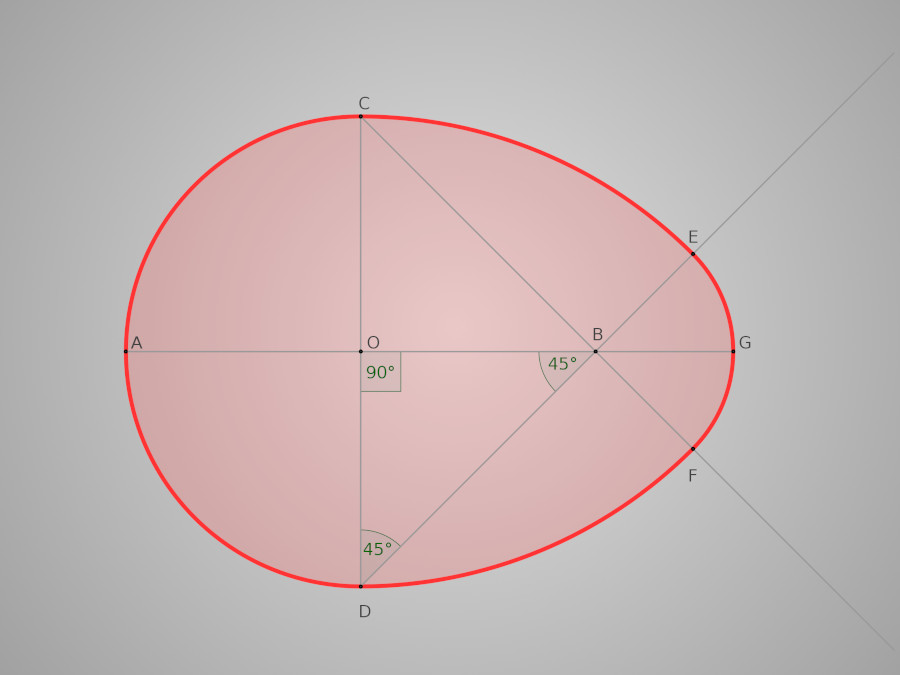
Calcul de la longueur

Soit R le rayon du cercle de départ et r le rayon du dernier arc tracé. La longueur de l'œuf sera donc égale à 2R+r. On connaît la valeur de R, il ne nous reste plus qu'à calculer celle de r. Ce rayon r est égal à la longueur BE et il est aisé de trouver cette longueur par le calcul : On a BE=DE-DB. On sait par construction que DE=DC=2R. Il ne nous reste plus qu'à trouver DB. On sait par construction que [OB] et [OD] sont perpendiculaires et que OB=OD=R. Il est donc facile de déterminer la longueur DB grace au théorème de Pythagore. DB²=OB²+OD²=2R² d'où DB=R√2. On a donc r=2R-R√2. Au final nous pouvons donc calculer la longueur AG à partir de R de la manière suivante : AG=2R+r=4R-R√2. Nous pouvons également déterminer les longueurs des différents arcs de cercles afin de calculer le périmètre de l'œuf et ainsi cuber le bois nécessaire à la fabrication. Je vous passe les détails ici, vous pourrez trouver tous ces calculs sur cette page bien détaillée du merveilleux site de Gérard Villemin.

Passons maintenant au deuxième tracé, celui qui va nous permettre d'obtenir un œuf un peu plus élancé, ce qui peut être pratique pour notre baignoire histoire d'avoir assez de longueur pour tendre les jambes sans avoir une baignoire trop large.

L'œuf du pentagone

Comme son nom l'indique, cet œuf est tracé à partir d'un pentagone. Attention pas n'importe quel pentagone : un pentagone régulier. C'est à dire un pentagone dont les cinq côtés sont de même longueur et dont les cinq angles internes ont la même mesure. Il existe de très nombreuses façons d'obtenir cette figure à la règle et au compas, je ne m'étendrai pas sur le sujet et me contenterai de vous présenter un tracé qui est de loin le plus simple et le plus rapide.

Commençons par tracer un cercle (celui dans lequel sera inscrit le pentagone) de centre O et de rayon [OB]. [AB] et [CD] sont deux diamètres perpendiculaires de ce cercle. Soit E le milieu de [OB]. Plaçons à présent sur le segment [AO] le point F tel que EF=EC.

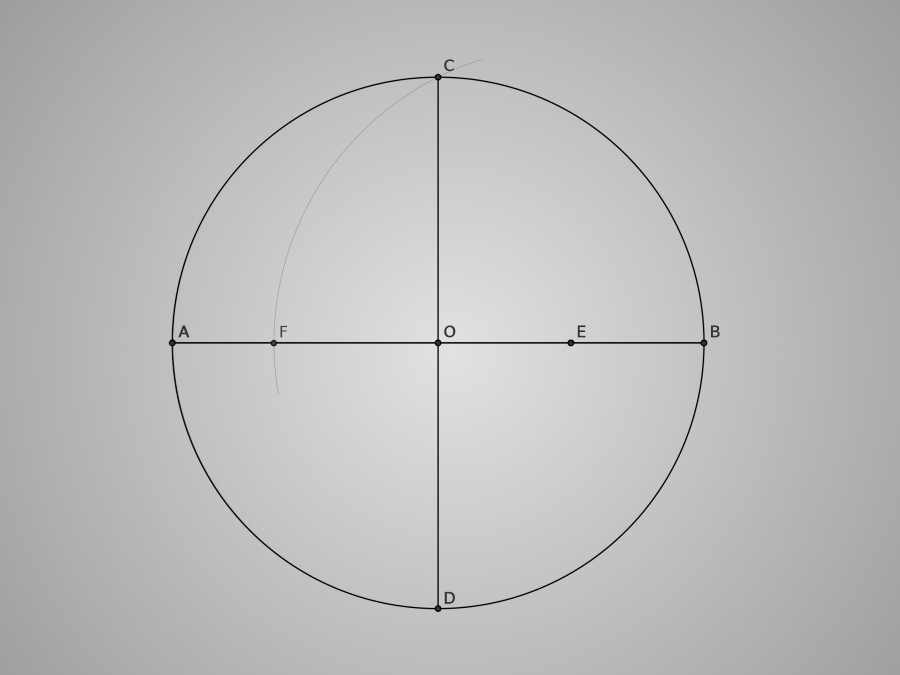
Traçons ensuite un arc de cercle de centre C et de rayon [CF]. Il coupe le cercle de départ en G et H. Nous obtenons ainsi trois sommets G, C et H du pentagone. L'arc de cercle de centre G et de rayon [GC] coupe le cercle en J. L'arc de cercle de centre H et de rayon [HC] coupe le cercle en I. Voici donc I et J, les deux sommets manquants.

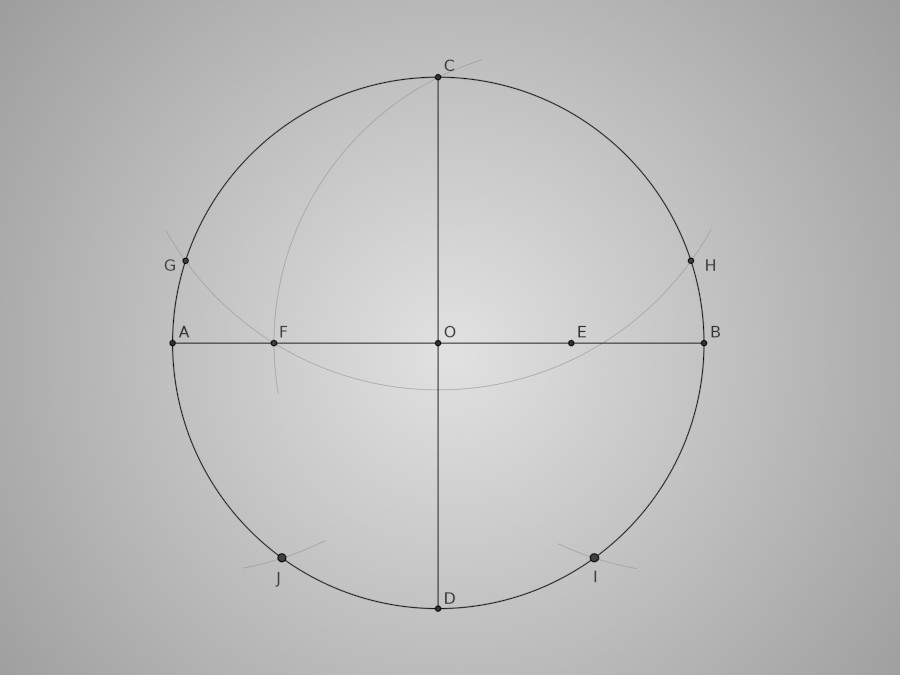
Il ne nous reste plus qu'à relier ces cinq somments afin de tracer le pentagone régulier CHIJG.

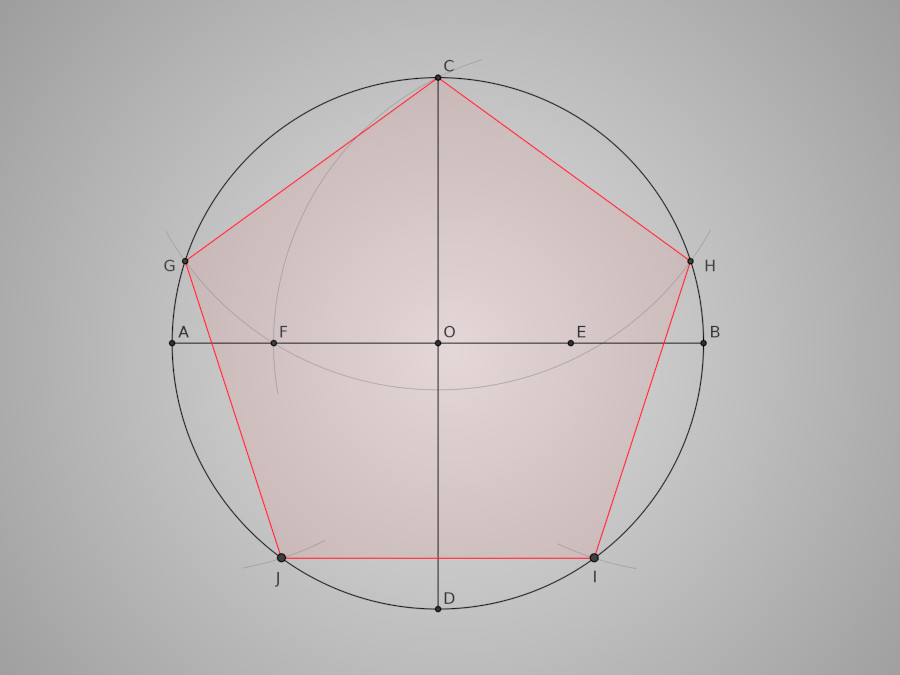
Traçons maintenant les cinq diagonales de ce pentagone. Les intersections de ces diagonales entre elles forment le pentagone régulier KLMNP dont nous allons également tracer les cinq diagonales.

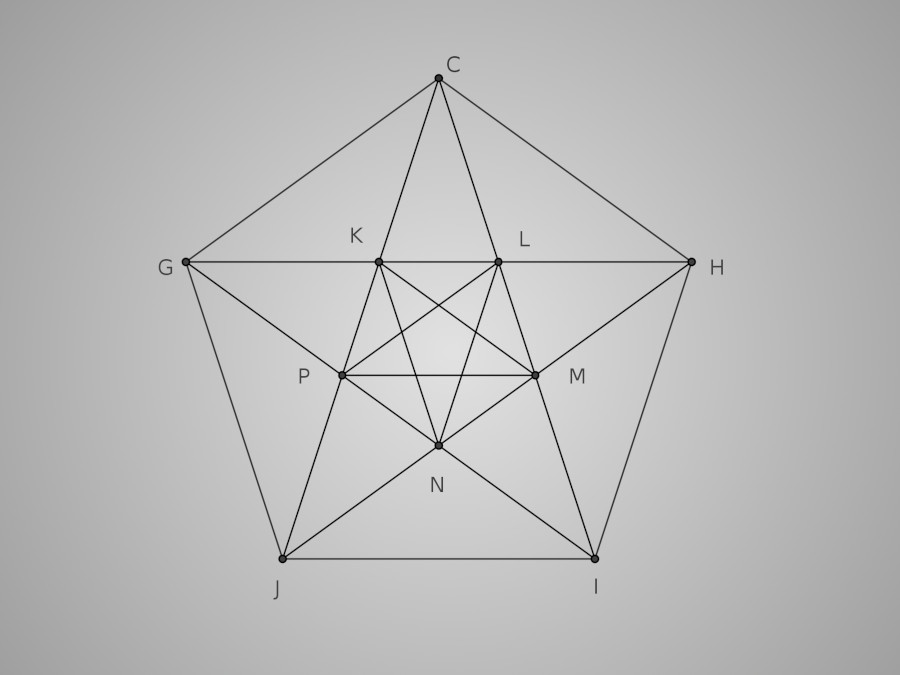
Nous y sommes presque, marquons S le point d'intersection des segments [KM] et [LP]. Prolongeons ces deux segment jusqu'à ce qu'ils coupent respectivement [HI] en R et [GJ] en Q. Nous avons à présent les quatre point Q R S et N qui sont les centres de notre tracé final. Traçons le segment [QR] ainsi que les points V et W, intersections de [QR] avec [CJ] et [CI], et faisons donc apparaître cet œuf !

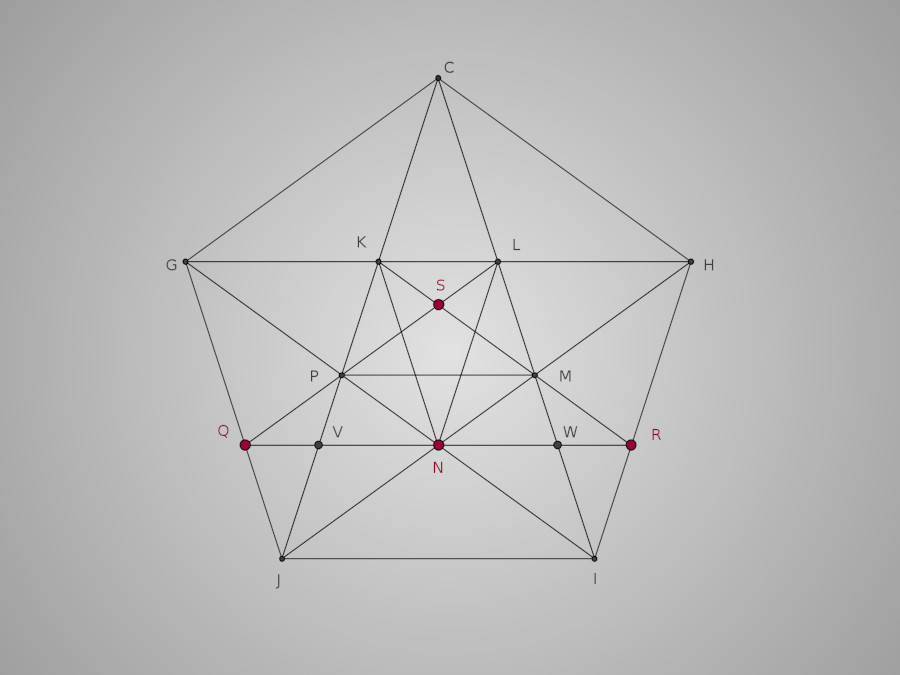
Nous pouvons commencer par tracer l'arc WV de centre N (qui est un demi-cercle)

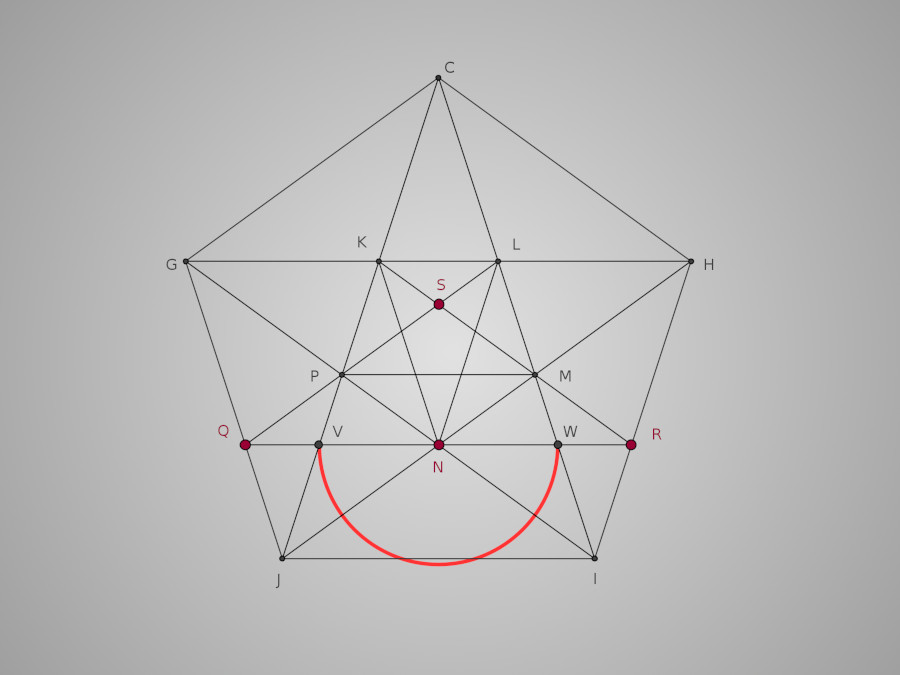
Poursuivons ensuite en traçant les deux grands arcs de l'œuf : l'arc VK de centre R et l'arc LW de centre Q.

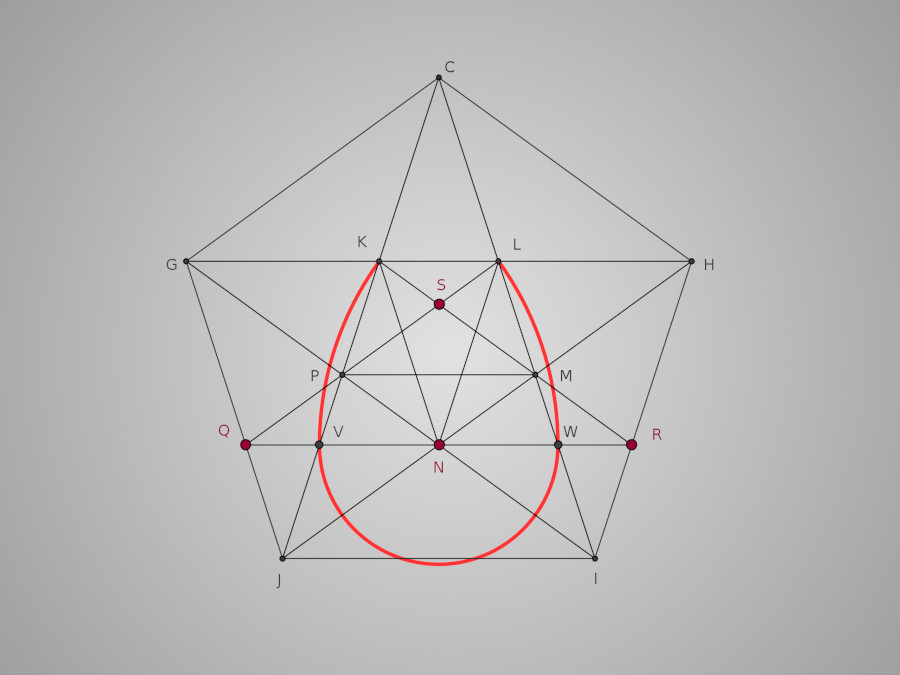
Pour finir il nous reste à tracer l'arc KL de centre S. Et voilà notre œuf complet !

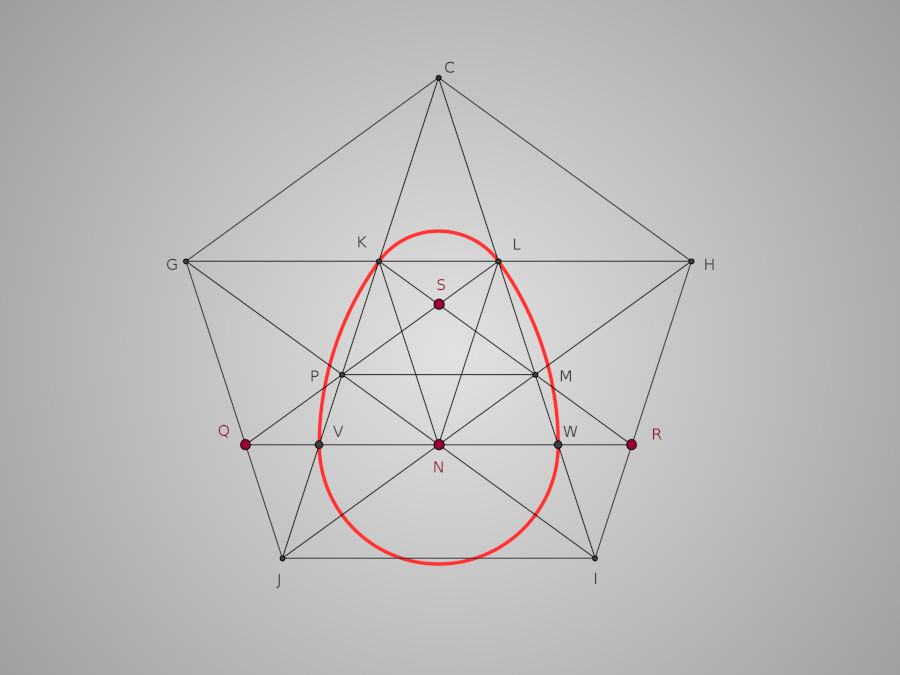
De la même manière que pour le tracé de l'anse de panier, nous voyons clairement l'intérêt ici au niveau des changements de pentes pour les angles de nos douves : les prolongements de [KS] et [VN ] passent par R et les prolongements de [LS] et [WN] passent par Q. Ainsi nous n'aurons pas à nous soucier des changements de pentes si ceux-ci sont correctement placés. Je vous explique tout ça en détail dans la vidéo ! Pour le moment, enlevons les traits de constructions et voyons à quoi ressemble notre œuf basé sur un pentagone régulier.