[VIDÉO] Géométrie : L'anse de panier

Quelquefois les tonneaux n'ont pas une section ronde mais ovale. Ça peut être utile par exemple pour fabriquer une baignoire, dont l'avantage sera alors d'être de belle dimension tout en ayant un encombrement moindre par rapport à une baignoire ronde. Comment faire pour fabriquer un cuveau de cette forme ? Tout commence par un tracé...

Ellipse - vs - Anse de panier

La forme ovale parfaite, c'est l'ellipse. Cette courbe fermée fait partie des coniques, c'est-à-dire qu'elle résulte de l'intersection d'un plan et d'un cône de révolution. En fonction de l'angle du plan par rapport à la pente du cône, nous obtiendrons une parabole, une hyperbole, ou une ellipse (ou un cercle d'ailleurs, mais le cercle est un cas particulier d'ellipse).

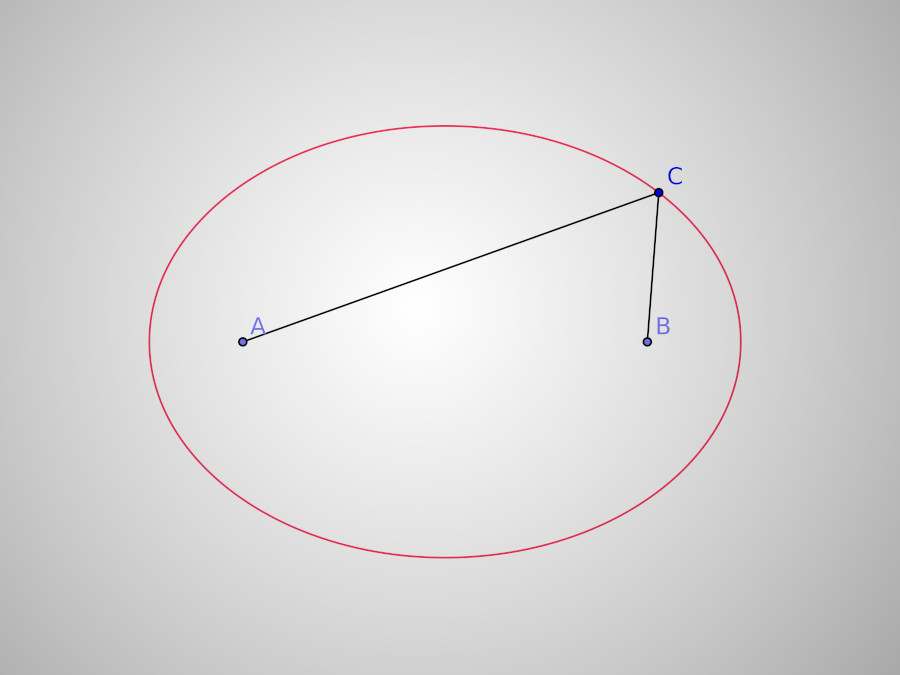
Une ellipse

Définition bifocale de l'ellipse : l'ellipse est le lieu des points dont la somme des distances à deux points fixes est constante. Sur le tracé ci-dessus nous avons une ellipse tracée en rouge. Les points A et B sont appelés "foyers" et la distance AC+CB est constante quel que soit l'endroit de l'ellipse où est placé C.
Fort bien, mais peut-on fabriquer une baignoire ovale de forme elliptique ? Non. Enfin si car tout est possible, mais ça serait vraiment très très pénible. En effet, pour déterminer l'angle à donner aux douves (le clain) nous avons besoin d'un point de centre. Or un arc d'ellipse n'a pas un point de centre mais deux foyers et la courbure de l'ellipse varie en permanence. Impossible donc de tracer la clé. Une solution serait de dessiner l'ellipse voulue en taille réelle et de jointer les douves de manière à suivre la courbe tracée. Pas bien pratique et il y a plus rapide.

La solution nous est donnée par le tracé de l'anse de panier, qui va nous permettre d'obtenir un ovale très proche de l'ellipse, plus facile à moduler, très harmonieux, et surtout beaucoup plus commode pour ce qu'on veut faire. En effet, le gros avantage de l'anse de panier est qu'elle est constituée d'arcs de cercles, elle permet donc de tracer et fabriquer aisément les calibres nécessaires.

Ci-dessous un ovale tracé avec la méthode de l'anse de panier, le premier dessin met en évidence le fait que cet ovale est composé d'arcs de cercles de différents diamètres, le deuxième dessin montre que la courbe obtenue est vraiment très proche de celle de l'ellipse.

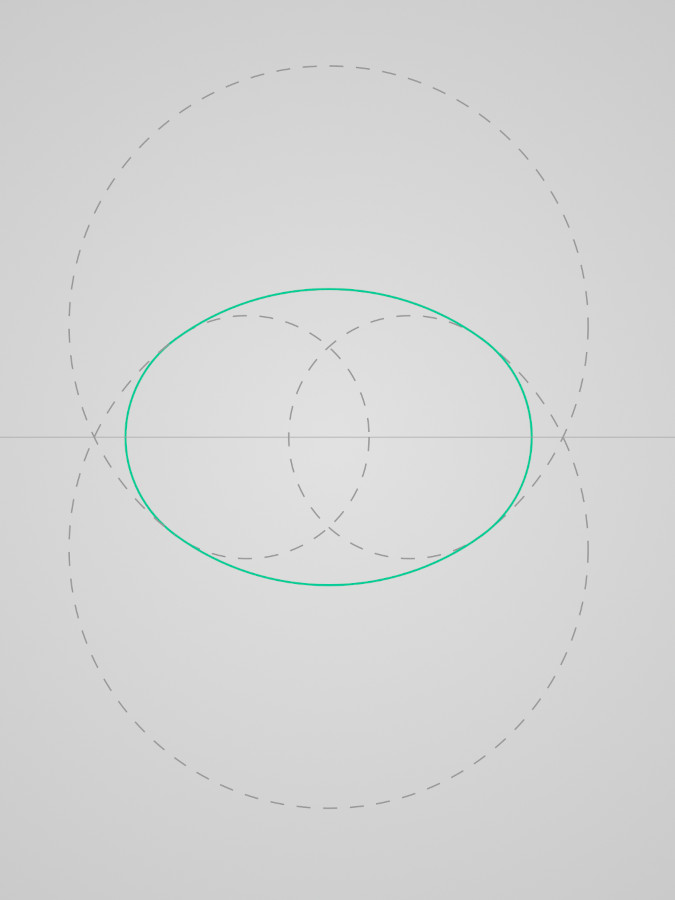
Ovale anse de panier

Comparaison des deux tracés

Le tracé

Partons d'un exemple concret. Je veux fabriquer une baignoire ovale aux dimensions suivantes : 150cm x 80cm. Je vais commencer par tracer un cercle de centre A et d'un diamètre égal à la longueur de cette baignoire, soit 150cm. Traçons le diamètre [BC] de ce cercle puis la droite (DE) perpendiculaire à [BC] passant par A. Plaçons sur cette droite un point F à la hauteur souhaitée de l'anse, la moitié de la largeur de l'ovale que l'on souhaite, donc, car cet ovale sera obtenu au final par une symétrie de l'anse par rapport à [BC]. Ici nous aurons donc AF=40cm. Voici posées les proportions de notre baignoire.

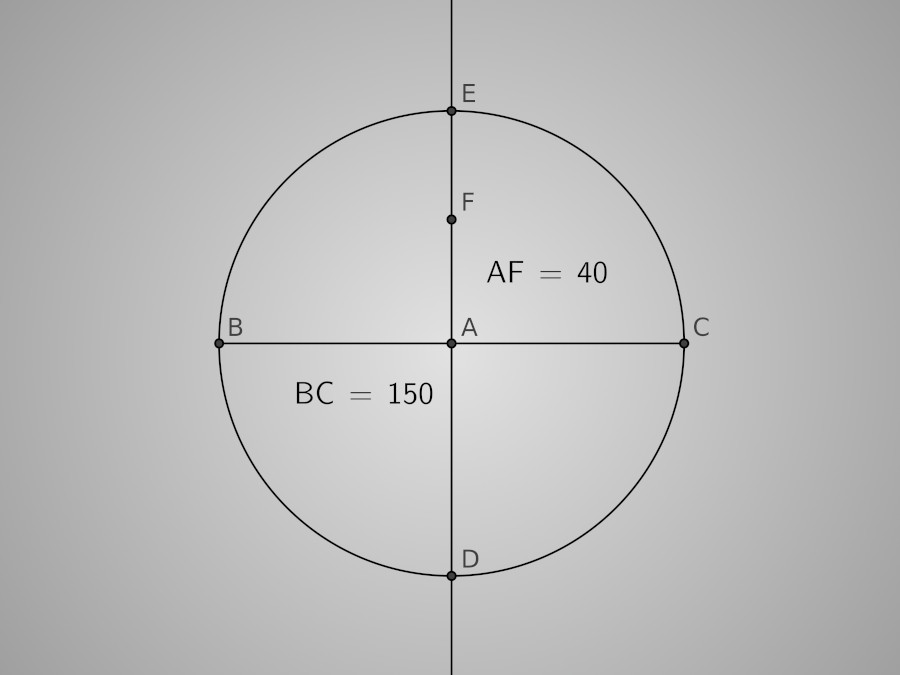
La base du tracé

Traçons maintenant un cercle de centre F et de rayon [FE] puis G le point d'intersection entre ce cercle et le segment [FB] et H le point d'intersection entre ce cercle et le segment [FC].

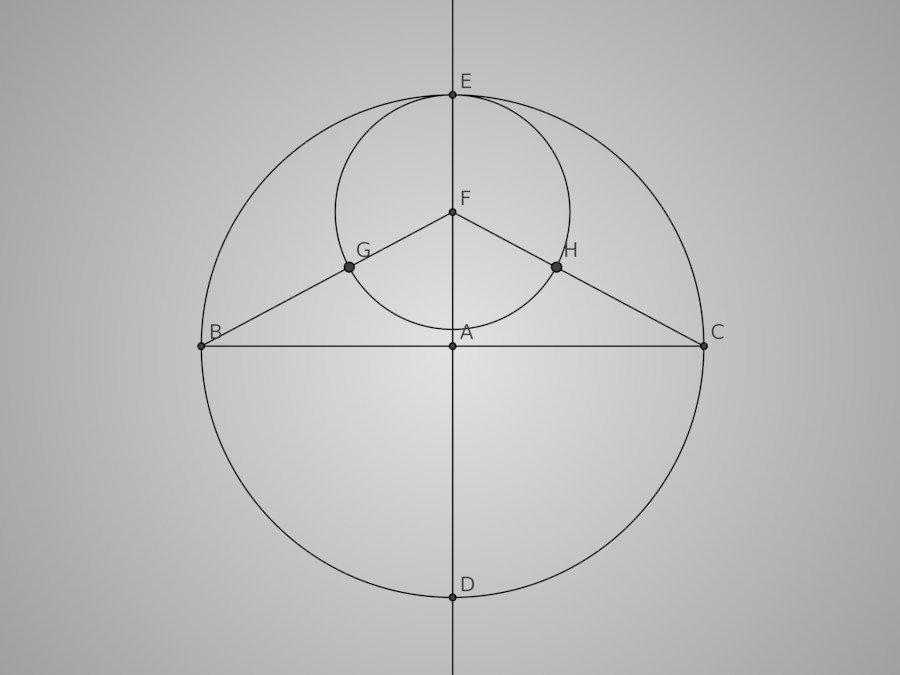
Étape 2

Pour finir, traçons les médiatrices des segments [BG] et [HC]. Ces médiatrices coupent [BC] respectivement en I et J et coupent également (DE) en K.

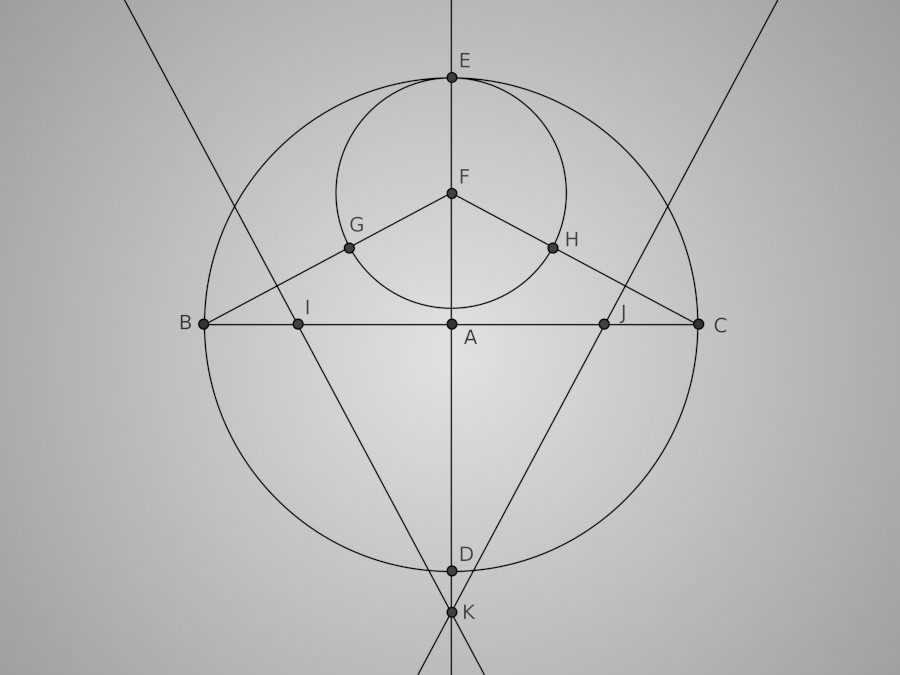
Les médiatrices

Nous y voilà ! Les points I J et K sont les trois points de centres des arcs de cercles qui vont nous permettre de tracer l'anse de panier. Traçons tout d'abord le grand arc de centre K et de rayon [KF]. Cet arc est délimité par les deux médiatrices qu'il coupe en L et M.

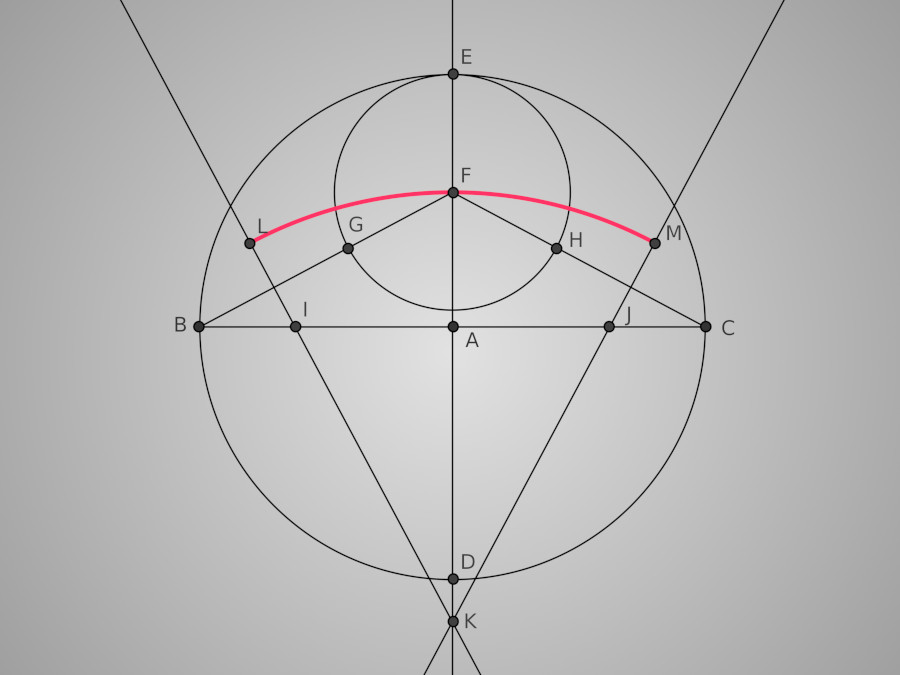
Le grand arc

Traçons à présent les deux petits arcs des extrémités. Il s'agit de l'arc BL de centre I et de rayon [IB] et de l'arc MC de centre J et de rayon [JC]. Notre anse de panier est tracée. Pour obtenir l'oval complet correspondant à notre baignoire il suffit de tracer une anse de panier symétrique à celle-ci par rapport à [BC] et le tour est joué !

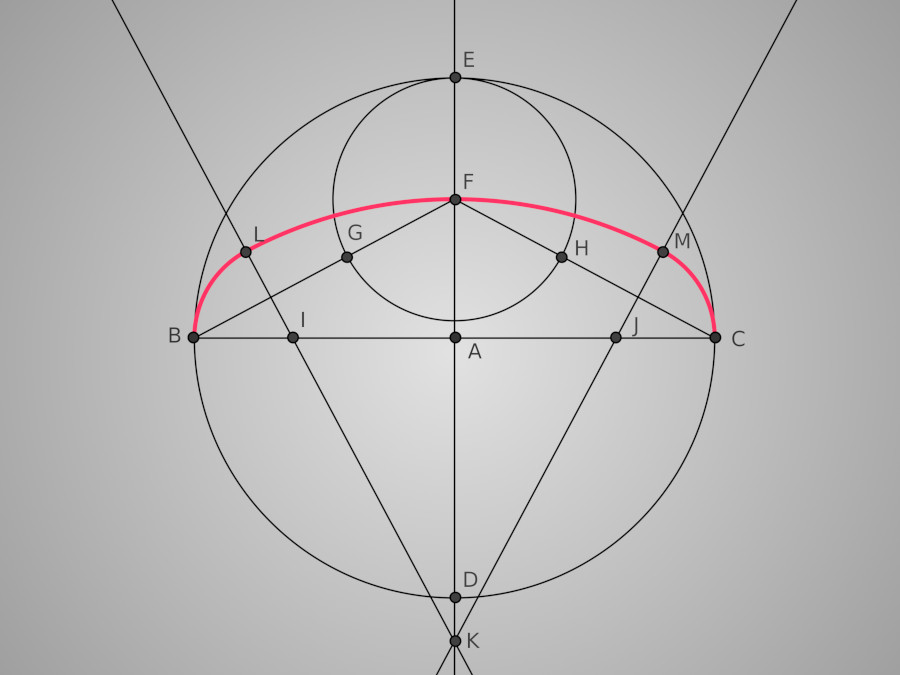
L'anse de panier complète

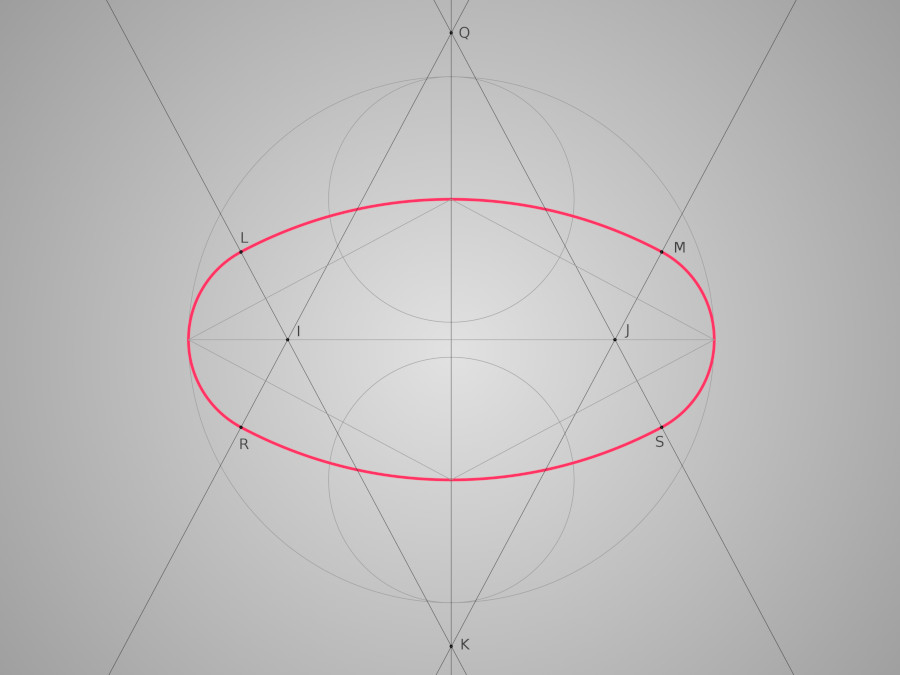
L'ovale obtenu par symétrie

L'intérêt de ce tracé

Vous avez compris le principe, fabriquer une baignoire purement elliptique n'a aucun intérêt car il serait impossible de tracer les calibres correspondants, alors qu'avec l'anse de panier on peut obtenir un ovale vraiment très semblable à l'ellipse et ça permet une fabrication avec seulement deux clés : une pour les arcs de grand rayon (la grande longueur de l'ovale) et une pour les petits arcs des extrémités. Oui mais voilà, la question qui se pose est la suivante : l'angle à donner à nos douves est très léger pour obtenir le grand arc, et au contraire très prononcé pour obtenir le petit arc. Alors comment passer de l'un à l'autre ? Comment faire la jonction et le changement d'angle permettant le changement de rayon ? C'est là que ce tracé devient magique car il résoud ce problème avec une simplicité déconcertante. Je m'explique : prenons par exemple le point L qui correspond au passage de l'arc RL à l'arc LM. Le point de centre de l'arc RL est le point I qui est déterminé par l'intersection de la médiatrice de [BG] avec [BC]. Et le point de centre du grand arc LM est situé à l'intersection de cette même médiatrice cette fois avec la droite (DE). Ce qui signifie que le rayon [LI] du petit arc et le rayon [LK] du grand arc sont deux segments d'une même droite : la médiatrice de [BG]. À l'endroit précis du point L, et uniquement à cet endroit, ces deux rayons se confondent donc et par conséquent nous n'avons pas à nous préoccuper d'un quelconque changement d'angle sur nos douves puisque c'est le même !

Pour notre fabrication il suffira donc de bien positionner les changements d'arcs aux points L M S et R et le tour sera joué ! Pour cela deux solutions : soit en faisant un tracé à l'échelle 1 et en présentant nos douves sur ce tracé, soit en mesurant nos différents arcs. Ces longueurs d'arcs sont très faciles à trouver par le calcul en fonction de l'ouverture de l'anse et de sa hauteur. Je ne vous fais pas le détail ici car vous pourrez trouver tout ça de manière très détaillée sur le net et qu'au final on n'est quand même pas là pour faire des maths hein...

Allez un début de piste, vous pouvez par exemple aller voir le site Mathématiques Magiques de Thérèse Éveilleau et en particulier cette page qui vous donnera plein d'infos sur l'anse de panier.

À vos compas !

- La vidéo -

-- Cyrille DUMOUTIER --