[VIDÉO] Fabrication artisanale d'un tonneau : Le litrage et les dimensions

Deuxième étape de la fabrication de notre fût de 50 litres cerclé bois. Aujourd'hui je vous présente quelques méthodes pour jauger un tonneau, c'est-à-dire calculer son litrage. À partir de ce calcul nous déterminerons les dimensions à donner à notre tonneau pour obtenir le litrage souhaité.

Un volume particulier

Le tonneau est un objet dont la forme est assez spéciale : en simplifiant on peut le voir comme deux troncs de cônes réunis par leur grande base, à ce détail près que la zone commune à ces deux troncs de cônes est cintrée. Cette courbure n'est pas répartie comme on pourrait le croire sur toute la longueur du fût mais uniquement au milieu, au niveau du plus grand diamètre. Cette zone se nomme le "bouge", et c'est elle qui pose problème pour le calcul du volume. En effet on ne peut pas se contenter de calculer le volume de deux troncs de cônes car ce calcul ne tient pas compte de la partie cintrée. On ne peut pas non plus tomber juste en considérant que la génératrice du tonneau est une parabole ou un arc d'ellipse car au contraire on ne tiendrait pas compte ici des parties non cintrées. En fait, il n'existe pas de formule mathématique exacte pour calculer son volume, mais qu'on se rassure, les résultats obtenus avec ces différentes méthodes sont très largement satisfaisants et la recherche de l'équation idéale n'a d'intérêt que par pure curiosité mathématique.

Quelques exemples de calcul

Pour toutes les formules qui suivent on notera:
L : la longueur intérieure du tonneau
D : le diamètre intérieur au niveau du bouge (plus grand diamètre)
d : le diamètre intérieur au niveau des fonds (plus petit diamètre)

1 - Les troncs de Cônes

Pour calculer le volume d'un tonneau correspondant à deux troncs de cônes, l'équation est la suivante :

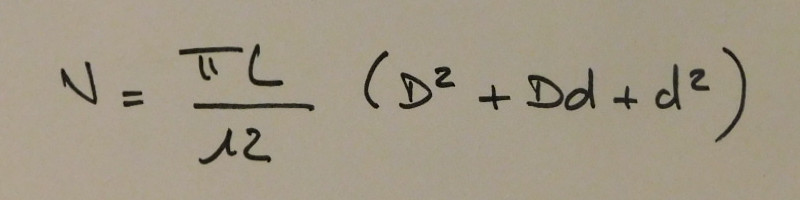
Troncs de cônes

L'inconvénient de ce calcul est qu'il ne tient pas compte de la partie cintrée, par conséquent le résultat obtenu sous-estime le litrage réel.

2 - Oughtred et Hutton

William Oughtred, mathématicien anglais (1574 - 1660) considère que le profil du tonneau est plus proche de l'ellipse. Aussi pour calculer son volume il propose l'équation suivante :

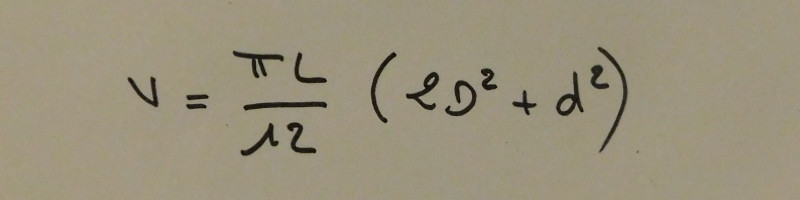
Equation de Oughtred

À l'inverse ce calcul surestime le litrage réel car il ne tient pas compte des parties droites du tonneau.
Charles Hutton (1737 - 1823) un autre mathématicien britannique proposera quant à lui la formule suivante :

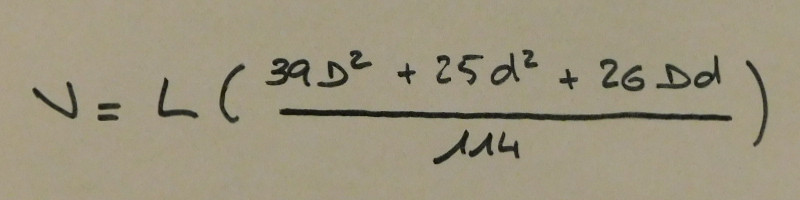
Equation de Hutton

3 - La Parabole

Sur le même principe on peut effectuer le calcul en considérant que la courbure du tonneau n'est plus une ellipse mais une parabole. L'équation est alors la suivante :

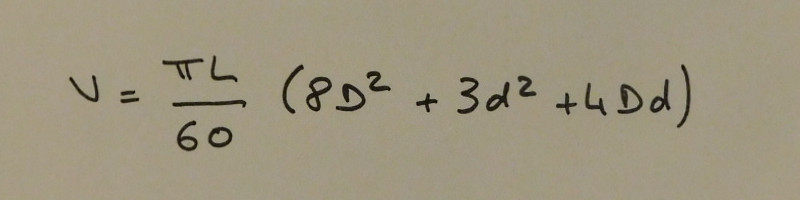
Equation basée sur la parabole

3 - Camus et Dez

Au XVIII^ème siècle la question préoccupe toujours bon nombre de mathématiciens. En 1741, dans les "Mémoires de mathématiques et physique de l'Académie Royale des Sciences", l'un d'entre eux M.Camus propose une forme bien plus cohérente du tonneau car elle tient compte à la fois de la courbure du bouge et des parties droites qui finissent le tonneau. Pour ses calculs il va donc considérer que le bouge du tonneau est un arc de parabole et qu'il est prolongé en ligne droite jusqu'au extrémités du fût par des tangentes à cette parabole. Voilà une représentation beaucoup plus proche de la réalité. L'équation correspondant à ce calcul est la suivante :

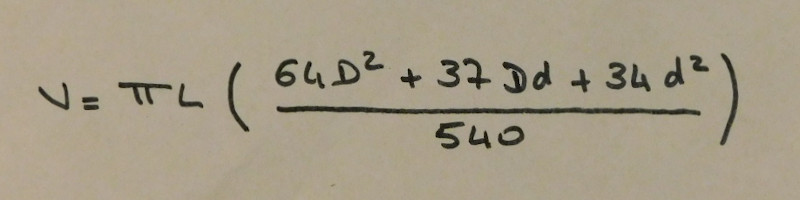
Equation de Camus

Le résultat obtenu est très juste mais les opérations à effectuer ne sont pas rapides, ce qui n'aide pas au problème quotidien du jaugeage. M.Dez, professeur royal de mathématiques à l'École Royale Militaire en proposera une version simplifiée dans son "Mémoire sur la théorie du Jaugeage" avec l'équation suivante :

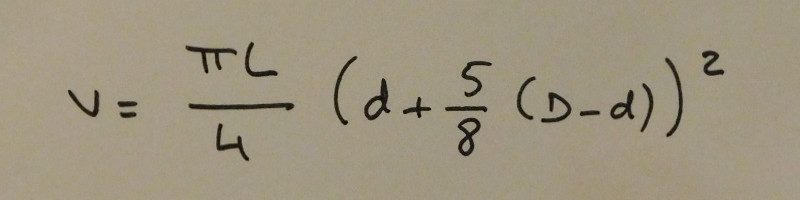
Equation de Dez

En 1806, M.Bazaine, professeur de jaugeage et contrôleur-jaugeur de l'Octroi de Bienfaisance de Paris, publie un "Cours de stéréométrie appliquée au jaugeage assujéti au système métrique". Au sujet de toutes les méthodes de calcul précédentes on peut lire : "tous les calculs faits d'après de pareilles estimations, et toutes les formules basées sur ces diverses hypothèses dont les résultats dans leur application n'étaient toujours qu'approximatifs, loin d'avoir atteint la précision que l'on cherchait à introduire dans l'art du jaugeage, n'ont fait que mieux sentir la difficulté d'y parvenir, et c'est ce qui a fait dire à l'un de ces savants qui s'en étaient sérieusement occupés, qu'il fallait que la pure géométrie se recusât de bonne grace sur le fait du jaugeage, et qu'elle en laissât le soin à la géométrie tâtonneuse et imparfaite."

Le principal problème vient du fait que les tonneaux ont des formes très variables, ils sont plutôt courts et trapus dans certaines régions, plus longs et élancés dans d'autres, et ces différences font qu'une formule correcte pour un tonneau ne le sera pas forcément pour un autre. Pour remédier à ce problème, l'instruction gouvernementale de pluviôse an VII (janvier-février 1799) impose une normalisation des proportions des tonneaux "de manière que la longueur intérieure, le diamètre du bouge et le diamètre des fonds fussent toujours dans le rapport des nombres 10,5 9 et 8". Cette instruction fournit également une nouvelle équation pour calculer le litrage : "les tonneaux doivent être calculés comme un cylindre qui aurait pour hauteur la longueur interne de la futaille, et pour diamètre, celui du bouge, moins le tiers de la différence qui se trouve entre ce diamètre et celui des fonds."
Ce qui nous donne l'équation suivante :

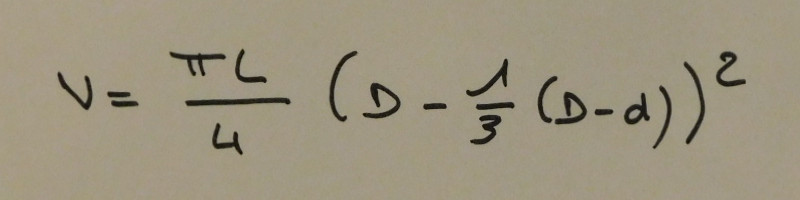
Pluviôse an VII

Très efficace pour simplifier le jaugeage mais trop compliqué à mettre en place. La futaille "métrique" ne se généralisera donc pas et tous les pays garderont leurs particularités. De nos jours encore, les tonneaux ont des proportions très différentes en fonction de leur provenance.

Oui mais alors que faire pour notre tonneau ? Toutes ces formules de calcul sont très intéressantes et très justes mais pour faciliter la tâche des tonneliers on a aussi trouvé des formules plus simples (tirées de cette fameuse "géométrie tâtonneuse et imparfaite" pour calculer rapidement le litrage d'un fût.
Celle-ci par exemple :

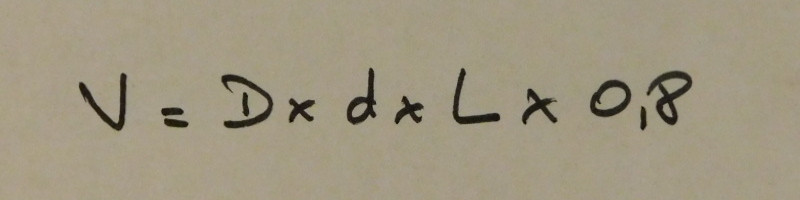
Calcul simplifié

Avantage : le calcul est rapide et facile, et le résultat est assez proche de la réalité avec un litrage un peu sous-estimé (environ 2% de moins que le litrage réel).

En bref vous n'avez que l'embarras du choix pour calculer le litrage d'un tonneau d'après ses dimensions. De préférence nous éliminerons les équations dont le résultat surestime ou sous-estime le litrage. J'ai tendance à bien aimer celles de Camus et de Dez qui correspondent le mieux à la forme réelle du tonneau. Concrètement, dans la vraie vie, je me suis fait une feuille de calcul avec toutes ces formules et il suffit ensuite de renseigner les dimensions intérieures du tonneau pour obtenir les différents résultats de litrages. Mais puisque le fût qu'on se propose de fabriquer ici sera aux proportions de la futaille métrique, utilisons donc la formule officielle du gouvernement ! Pour le coup il est même inutile de faire le calcul car l'instruction de Pluviôse An VII fournit un tableau des principales contenances des futailles métriques.

Futaille métrique

Notre fût de 50 litres aura donc pour dimensions 454 millimètres de longueur intérieure, 389 millimètres de diamètre au niveau du bouge, et 345 millimètres de diamètre au niveau des fonds. Attention à ne pas faire d'erreur, il s'agit ici des dimensions intérieures. Il conviendra donc pour obtenir les dimensions extérieures (que nous allons utiliser pour tracer la clé) d'ajouter à ces diamètres deux fois l'épaisseur du bois, et à cette longueur deux fois la largeur du jable et deux fois la longueur des peignes (la partie des douelles qui se trouve après les jables). Il faut ajouter encore un peu de longueur pour prendre en compte la courbure de la douelle (Pythagore est votre ami...). Au final pour un tonneau dont le bois aura 20 millimètres d'épaisseur, on peut fixer comme dimensions extérieures les cotes suivantes:

Longueur des douves: 560 millimètres (oui je sais, dans la vidéo je dis 584, je me suis un peu emporté sur la longueur des peignes...)
Diamètre aux fonds: 385 millimètres
Diamètre au bouge: 429 millimètres

Bien évidemment vous pouvez obtenir le même litrage en donnant d'autres proportions à votre tonneau. Faites vos calculs, vous pouvez également aller visiter le site Mathématiques Magiques, où vous trouverez entre beaucoup d'autres merveilles une jauge à tonneaux pour faire vos tests de litrages.

La vidéo

-- Cyrille DUMOUTIER --